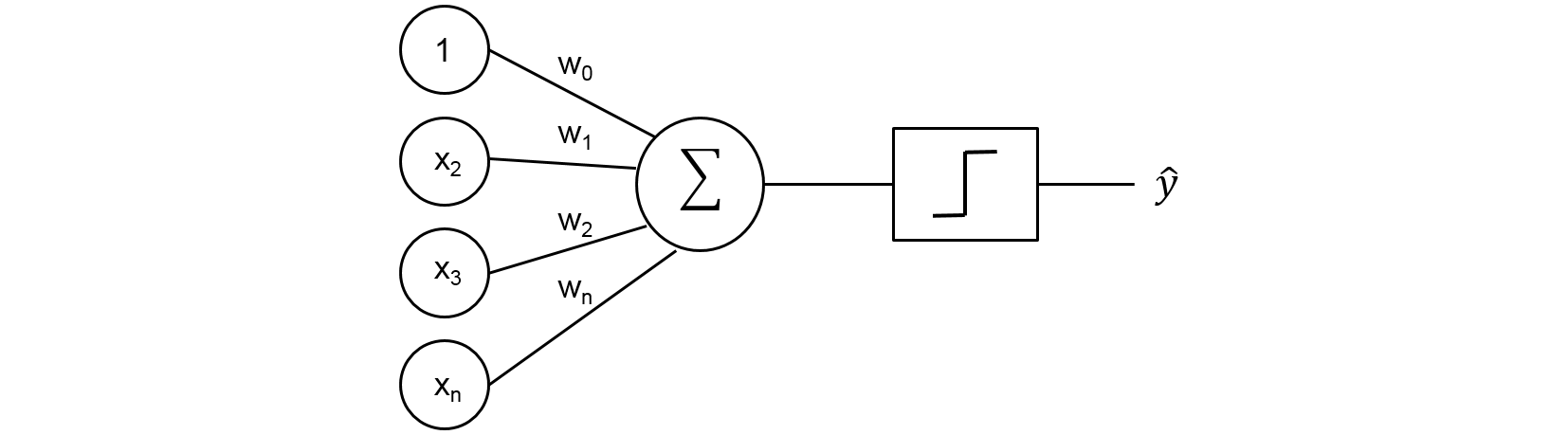
World-Happiness Multiple Linear Regression
project 3- DSC680
Happiness 2020
soukhna Wade 11/01/2020
Introduction
There are three parts of the report as follows:
Cleaning
Visualization
Multiple Linear Regression in Python
The purpose of choosing this work is to find out which factors are more important to live a happier life. As a result, people and countries can focus on the more significant factors to achieve a higher happiness level. We also will implement several machine learning algorithms to predict the happiness score and compare the result to discover which algorithm works better for this specific dataset.
https://www.kaggle.com/mathurinache/world-happiness-report?select=2020.csv
https://www.kaggle.com/pinarkaya/world-happiness-eda-visualization-ml#2019-Data
Import necessary Libraries
# Standard library import-Python program# for some basic operations
import pandas as pd
import numpy as np # linear algebra
import matplotlib.pyplot as plt # for graphics
import seaborn as sns # for visualizations
plt.style.use('fivethirtyeight')
import seaborn as seabornInstance
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics
# Use to configure display of graph
%matplotlib inline
#stop unnecessary warnings from printing to the screen
import warnings
warnings.simplefilter('ignore')
# for interactive visualizations
import plotly.offline as py
from plotly.offline import init_notebook_mode, iplot
import plotly.graph_objs as go
init_notebook_mode(connected = True)
Import and read Dataset from local library
#The following command imports the CSV dataset using pandas:
import pandas as pd
happyness_2020 = pd.read_csv("happyness_2020.csv")
happyness_2020.head(1)
| Country name | Regional indicator | Ladder score | Standard error of ladder score | upperwhisker | lowerwhisker | Logged GDP per capita | Social support | Healthy life expectancy | Freedom to make life choices | Generosity | Perceptions of corruption | Ladder score in Dystopia | Explained by: Log GDP per capita | Explained by: Social support | Explained by: Healthy life expectancy | Explained by: Freedom to make life choices | Explained by: Generosity | Explained by: Perceptions of corruption | Dystopia + residual | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Finland | Western Europe | 7.8087 | 0.031156 | 7.869766 | 7.747634 | 10.639267 | 0.95433 | 71.900825 | 0.949172 | -0.059482 | 0.195445 | 1.972317 | 1.28519 | 1.499526 | 0.961271 | 0.662317 | 0.15967 | 0.477857 | 2.762835 |
#happyness_2020.columns
Looking at the current shape of the dataset under consideration
# Looking at the current shape of the dataset under consideration
#df.shape
# Step 2: check the dimension of the table or the size of dataframe
print("The dimension of the table is: ",happyness_2020.shape)
The dimension of the table is: (153, 20)
Cleaning - Is threre any missing or null Values in this dataset (happyness_2020)?
In this section, we load our dataset and see the structure of happiness variables. Our dataset is pretty clean, and we will implement a few adjustments to make it looks better.
#check for any missing values or null values (NA or NaN)
happyness_2020 .isnull().sum()
#df.isnull().head(6)
Country name 0
Regional indicator 0
Ladder score 0
Standard error of ladder score 0
upperwhisker 0
lowerwhisker 0
Logged GDP per capita 0
Social support 0
Healthy life expectancy 0
Freedom to make life choices 0
Generosity 0
Perceptions of corruption 0
Ladder score in Dystopia 0
Explained by: Log GDP per capita 0
Explained by: Social support 0
Explained by: Healthy life expectancy 0
Explained by: Freedom to make life choices 0
Explained by: Generosity 0
Explained by: Perceptions of corruption 0
Dystopia + residual 0
dtype: int64
** Note that in the above result no missing values so, the dataset is pretty cleaned.**
# Print a list datatypes of all columns
happyness_2020.head(1)
| Country name | Regional indicator | Ladder score | Standard error of ladder score | upperwhisker | lowerwhisker | Logged GDP per capita | Social support | Healthy life expectancy | Freedom to make life choices | Generosity | Perceptions of corruption | Ladder score in Dystopia | Explained by: Log GDP per capita | Explained by: Social support | Explained by: Healthy life expectancy | Explained by: Freedom to make life choices | Explained by: Generosity | Explained by: Perceptions of corruption | Dystopia + residual | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Finland | Western Europe | 7.8087 | 0.031156 | 7.869766 | 7.747634 | 10.639267 | 0.95433 | 71.900825 | 0.949172 | -0.059482 | 0.195445 | 1.972317 | 1.28519 | 1.499526 | 0.961271 | 0.662317 | 0.15967 | 0.477857 | 2.762835 |
Exploratory Data Analysis
Prints information of all columns:
happyness_2020 .info() # Prints information of all columns:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 153 entries, 0 to 152
Data columns (total 20 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Country name 153 non-null object
1 Regional indicator 153 non-null object
2 Ladder score 153 non-null float64
3 Standard error of ladder score 153 non-null float64
4 upperwhisker 153 non-null float64
5 lowerwhisker 153 non-null float64
6 Logged GDP per capita 153 non-null float64
7 Social support 153 non-null float64
8 Healthy life expectancy 153 non-null float64
9 Freedom to make life choices 153 non-null float64
10 Generosity 153 non-null float64
11 Perceptions of corruption 153 non-null float64
12 Ladder score in Dystopia 153 non-null float64
13 Explained by: Log GDP per capita 153 non-null float64
14 Explained by: Social support 153 non-null float64
15 Explained by: Healthy life expectancy 153 non-null float64
16 Explained by: Freedom to make life choices 153 non-null float64
17 Explained by: Generosity 153 non-null float64
18 Explained by: Perceptions of corruption 153 non-null float64
19 Dystopia + residual 153 non-null float64
dtypes: float64(18), object(2)
memory usage: 24.0+ KB
Display some statistical summaries of the numerical columns data. To see the statistical details of the dataset, we can use describe():
happyness_2020 .describe().head(1) # display some statistical summaries of the numerical columns data.
| Ladder score | Standard error of ladder score | upperwhisker | lowerwhisker | Logged GDP per capita | Social support | Healthy life expectancy | Freedom to make life choices | Generosity | Perceptions of corruption | Ladder score in Dystopia | Explained by: Log GDP per capita | Explained by: Social support | Explained by: Healthy life expectancy | Explained by: Freedom to make life choices | Explained by: Generosity | Explained by: Perceptions of corruption | Dystopia + residual | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 | 153.0 |
#happyness_2020.columns # display the list of the columns
Let us examine the data for the county very happy and the one that is not
maxSupport=np.max(happyness_2020["Social support"])
maxSupport
0.9746695759999999
maxEconomy=np.max(happyness_2020["Logged GDP per capita"])
maxEconomy
11.45068073
happyness_2020[happyness_2020['Ladder score']==np.max(happyness_2020['Ladder score'])]['Country name']
0 Finland
Name: Country name, dtype: object
maxSupport=np.min(happyness_2020["Social support"])
maxSupport
0.31945985600000004
minEconomy=np.min(happyness_2020["Logged GDP per capita"])
minEconomy
6.492642403
happyness_2020[happyness_2020['Ladder score']==np.min(happyness_2020['Ladder score'])]['Country name']
152 Afghanistan
Name: Country name, dtype: object
To rename columns
happyness_2020 .rename(columns={"Country name":"Country",
"Logged GDP per capita":"GDP per capita",
"Explained by: Healthy life expectancy":"Health",
"Freedom to make life choices":"Freedom",
"Overall rank":"Happiness Rank"},inplace=True)
#happyness_2020 .columns
Removing unnecessary columns (Freedom to make life choices and Healthy life expectancy)
#''' drop multiple column based on name in pandas'''
d2020=happyness_2020.drop(['Regional indicator','Standard error of ladder score', 'upperwhisker', 'lowerwhisker',
'Ladder score in Dystopia', 'Explained by: Social support',
'Explained by: Freedom to make life choices',
'Explained by: Generosity', 'Explained by: Perceptions of corruption',
'Dystopia + residual','Explained by: Log GDP per capita'], axis='columns')
d2020.head(1)
| Country | Ladder score | GDP per capita | Social support | Healthy life expectancy | Freedom | Generosity | Perceptions of corruption | Health | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Finland | 7.8087 | 10.639267 | 0.95433 | 71.900825 | 0.949172 | -0.059482 | 0.195445 | 0.961271 |
d2020.shape
(153, 9)
d2020.columns
Index(['Country', 'Ladder score', 'GDP per capita', 'Social support',
'Healthy life expectancy', 'Freedom', 'Generosity',
'Perceptions of corruption', 'Health'],
dtype='object')
d2020.head(1)
| Country | Ladder score | GDP per capita | Social support | Healthy life expectancy | Freedom | Generosity | Perceptions of corruption | Health | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Finland | 7.8087 | 10.639267 | 0.95433 | 71.900825 | 0.949172 | -0.059482 | 0.195445 | 0.961271 |
Visualization
The correlation of the variables of the dataset - Heatmap
fig, ax = plt.subplots()
fig.set_size_inches(15, 10)
sns.heatmap(happyness_2020 .corr(),cmap='coolwarm',ax=ax,annot=True,linewidths=2)
<matplotlib.axes._subplots.AxesSubplot at 0x20db1c630d0>

There is an inverse correlation between “Ladder score” and all the other numerical variables. The lower the happiness score, the higher the score, and the higher the other factors that contribute to happiness.
The correlation of the new dataset after renaming and droping columns- Heatmap
#The correlation of the new dataset
fig, ax = plt.subplots()
fig.set_size_inches(15, 10)
sns.heatmap(d2020.corr(),cmap='coolwarm',ax=ax,annot=True,linewidths=2)
<matplotlib.axes._subplots.AxesSubplot at 0x20db23735b0>

According to the above correlation plot, GPA per capita, social support, and healthy life expectancy play the most significant role in contributing to happiness. While perceptions of corruption have the lowest impact on the happiness score.
Let’s see relationship between different features with happiness score.
1. GDP per capita
Relationship between GDP per capita(Economy of country) has postive strong relationship with happiness score. So If GDP per Capita of a country is high than Happiness Score of that country also more likely to be high.
#https://www.kaggle.com/dgtech/world-happiness-with-basic-visualization-and-eda
import matplotlib.pyplot as plt
import seaborn as sb
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
happyness_2020 = pd.read_csv("happyness_2020.csv")
plt.figure(figsize=(14,7))
plt.title("Ladder Score vs Logged GDP per capita")
sb.regplot(data=happyness_2020, x='Logged GDP per capita', y='Ladder score');

Using the histogram helps us to make the decision making process a lot more easy to handle by viewing the data that was collected
d2020.hist()
array([[<matplotlib.axes._subplots.AxesSubplot object at 0x0000020DB3454A00>,
<matplotlib.axes._subplots.AxesSubplot object at 0x0000020DB34C91C0>,
<matplotlib.axes._subplots.AxesSubplot object at 0x0000020DB34F5610>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x0000020DB3521A60>,
<matplotlib.axes._subplots.AxesSubplot object at 0x0000020DB354DEB0>,
<matplotlib.axes._subplots.AxesSubplot object at 0x0000020DB3584280>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x0000020DB3584370>,
<matplotlib.axes._subplots.AxesSubplot object at 0x0000020DB35B1820>,
<matplotlib.axes._subplots.AxesSubplot object at 0x0000020DB3619070>]],
dtype=object)

How is the Happiness Score is distributed?
As you can see below ladder score (happiness score) has values above 2.50 and below 7.77. So there is no single country which has a happiness score above 8.
sns.distplot(d2020['Ladder score'])
d2020.head(1)
| Country | Ladder score | GDP per capita | Social support | Healthy life expectancy | Freedom | Generosity | Perceptions of corruption | Health | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Finland | 7.8087 | 10.639267 | 0.95433 | 71.900825 | 0.949172 | -0.059482 | 0.195445 | 0.961271 |

Top 6 Countries with high GDP (Economy)
plt.figure(figsize=(14,7))
plt.title("Top 6 Countries with High GDP")
sb.barplot(data = happyness_2020.sort_values('Logged GDP per capita', ascending= False).head(6), y='Logged GDP per capita', x='Country name')
plt.xticks(rotation=90);

2. Perceptions of corruption
Distribution of Perceptions of corruption rightly skewed, which means very less number of country has high perceptions of corruption. That means most of the country has corruption problem.
Corruption is a very big problem for the word. How corruption can impact on Happiness Score?
Perceptions of corruption data is highly skewed no wonder why the data has weak linear relationship, but as you can see in scatter plot most of the data points are on left side and most of the countries with low perceptions of corruption has happiness score between 4 to 6.
Countries with high perception score has high happiness score above 7.
plt.figure(figsize= (15,7))
plt.subplot(1,2,1)
plt.title("Perceptions of corruption distribution")
sb.distplot(a=happyness_2020['Perceptions of corruption'], bins =np.arange(0, 0.45+0.2,0.05))
plt.ylabel('Count')
plt.subplot(1,2,2)
plt.title("Happiness Score vs Perceptions of corruption")
sb.regplot(data=happyness_2020, x='Perceptions of corruption', y='Ladder score');

Top 6 Countries with high Perceptions of corruption in the year 2020
plt.figure(figsize=(14,7))
plt.title("Top 6 Countries with High Perceptions of corruption in the year")
sb.barplot(data =happyness_2020.sort_values('Perceptions of corruption', ascending= False).head(6), x='Country name', y='Perceptions of corruption')
plt.xticks(rotation=90);

3. Healthy life expectancy
A healthy life expectancy has a strong and positive relationship with a happiness score. If a country has a high life expectancy that means it can also have a high happiness score. It makes sense because anyone who has a very long healthy life he/she is happy. Everyone likes to get a healthy and long life aren’t you?
plt.figure(figsize=(14,7))
plt.title("Happiness Score vs Healthy life expectancy")
sb.regplot(data=happyness_2020, x='Healthy life expectancy', y='Ladder score');

Top 6 Countries with high Healthy life expectancy in the year 2020
plt.figure(figsize=(14,7))
plt.title("Top 6 Countries with High Healthy life expectancy in the year 2020")
sb.barplot(data = happyness_2020.sort_values('Healthy life expectancy', ascending= False).head(6), x='Country name', y='Perceptions of corruption')
plt.xticks(rotation=90);

4. Social Support
Social support of countries also has a strong and positive relationship with happiness scores. Also, the relationship with happiness or ladder score needs to be strong because the more you will help socially more you will be happy.
Social support measures the perception that one has assistance available, the received assistance, or the degree to which a person can integrate into a social network. Support can come from many sources, such as family, friends, pets, neighbors, coworkers, etc.
import matplotlib.pyplot as plt
import seaborn as sb
import warnings
import pandas as pd
happyness_2020 = pd.read_csv("happyness_2020.csv")
warnings.filterwarnings('ignore')
plt.figure(figsize=(14,7))
plt.title("Happiness Score vs Social Support")
sb.regplot(data=happyness_2020, x='Social support', y='Ladder score');

Top 6 Countries with high Social Support in year 2020
plt.figure(figsize=(14,7))
plt.title("Top 6 Countries with Social Support")
sb.barplot(data = happyness_2020.sort_values('Social support', ascending= False).head(6), x='Country name', y='Social support')
plt.xticks(rotation=90);

Freedom to make life choices
“Freedom to make life choices” is the national average of responses to the question “Are you satisfied or dissatisfied with your freedom to choose what you do with your life?”
Freedom to make life choices has some positive relationships with happiness scores. This relation makes sense because the more you will get free to make decisions about your life, the more you will be happy.
plt.figure(figsize=(14,7))
plt.title("Happiness Score vs Freedom to make life choices")
sb.regplot(data=happyness_2020, x='Freedom to make life choices', y='Ladder score');

The top 6 countries with high freedom to make life choices
plt.figure(figsize=(14,7))
plt.title("Top 6 Countries with High Freedom to make life choices")
sb.barplot(data = happyness_2020.sort_values('Freedom to make life choices', ascending= False).head(6), x='Country name', y='Freedom to make life choices')
plt.xticks(rotation=90);

6. Generosity
The generosity and life expectancy are among the six variables scientists peek at when making the World Happiness Report.
Generosity has a weak linear relationship with the ladder score. One can ask a question:” Why the word “generosity” has not a linear relationship with happiness score?
The reason is that the generosity score depends on the countries that can give the most to nonprofits around the world. Countries which are not generous that does not mean they are not happy.
plt.figure(figsize=(14,7))
plt.title("Happiness Score vs Generosity")
sb.regplot(data=happyness_2020, x='Generosity', y='Ladder score');

The top 6 countries with high generosity
plt.figure(figsize=(14,7))
plt.title("The Top 6 Countries with High Generosity")
sb.barplot(data = happyness_2020.sort_values('Generosity', ascending= False).head(6), x='Country name', y='Generosity')
plt.xticks(rotation=90);

How one feature is related to another feature?
#p = sb.PairGrid(happyness_2020)
#p.map_diag(plt.hist)
#p.map_offdiag(plt.scatter);
Multiple Linear Regression in Python
It is the most common form of Linear Regression. Multiple Linear Regression describes how a single response variable Y depends linearly on a number of predictor variables. Consider ‘Ladder score’ as the dependent variable and the rest of the attributes as independent variables.
It is the most common form of Linear Regression. Multiple Linear Regression basically describes how a single response variable Y depends linearly on a number of predictor variables.
Step 1:Have a glance at the shape
d2020.shape
(153, 9)
#Have a look at the data first five row
d2020.head()
#d2020.columns
| Country | Ladder score | GDP per capita | Social support | Healthy life expectancy | Freedom | Generosity | Perceptions of corruption | Health | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Finland | 7.8087 | 10.639267 | 0.954330 | 71.900825 | 0.949172 | -0.059482 | 0.195445 | 0.961271 |
| 1 | Denmark | 7.6456 | 10.774001 | 0.955991 | 72.402504 | 0.951444 | 0.066202 | 0.168489 | 0.979333 |
| 2 | Switzerland | 7.5599 | 10.979933 | 0.942847 | 74.102448 | 0.921337 | 0.105911 | 0.303728 | 1.040533 |
| 3 | Iceland | 7.5045 | 10.772559 | 0.974670 | 73.000000 | 0.948892 | 0.246944 | 0.711710 | 1.000843 |
| 4 | Norway | 7.4880 | 11.087804 | 0.952487 | 73.200783 | 0.955750 | 0.134533 | 0.263218 | 1.008072 |
Step 2: Have a glance at the dependent and independent variables
import pandas as pd
# predictores
#x = d2020[['GDP per capita', 'Social support',
# 'Healthy life expectancy', 'Freedom', 'Generosity',
# 'Perceptions of corruption', 'Economy', 'Health']]
x=pd.DataFrame(d2020.iloc[:,2 :])
x.head(3)
| GDP per capita | Social support | Healthy life expectancy | Freedom | Generosity | Perceptions of corruption | Health | |
|---|---|---|---|---|---|---|---|
| 0 | 10.639267 | 0.954330 | 71.900825 | 0.949172 | -0.059482 | 0.195445 | 0.961271 |
| 1 | 10.774001 | 0.955991 | 72.402504 | 0.951444 | 0.066202 | 0.168489 | 0.979333 |
| 2 | 10.979933 | 0.942847 | 74.102448 | 0.921337 | 0.105911 | 0.303728 | 1.040533 |
# target feature or dependable variable
#y = d2020['Ladder score']
y=pd.DataFrame(d2020.iloc[:, 1])
y.head(3)
Index(['Country', 'Ladder score', 'GDP per capita', 'Social support',
'Healthy life expectancy', 'Freedom', 'Generosity',
'Perceptions of corruption', 'Health'],
dtype='object')
Step 3: Visualize the change in the variables
# Step 4: Visualize the change in the variables
import matplotlib.pyplot as plt
d2020.plot(x ='Health', y ='Ladder score', style ='o' )
plt.xlabel('Health')
plt.ylabel('Ladder score')
plt.show()

Step 4: Divide the data into train and test sets
#Divide the data into train and test sets:
x_train, x_test, y_train, y_test, = train_test_split(x,y,test_size=0.3, random_state=10, shuffle=True)
Step 5: Have a glance at the shape of the train and test sets:
#Have a glance at the shape of the train and test sets:
print(x_train.shape)
print(x_test.shape)
print(y_train.shape)
print(y_test.shape)
(107, 7)
(46, 7)
(107, 1)
(46, 1)
Step 6: Train the algorithm
from sklearn.linear_model import LinearRegression
# Regression model
regressor = LinearRegression()
# Fitting the data to my model
#model = regression.fit(x_train, y_train)
regressor.fit(x_train, y_train)
LinearRegression()
Step 7:Having a look at the coefficients that the model has chosen
# Having a look at the coefficients that the model has chosen:
import pandas as pd
v = pd.DataFrame(regressor.coef_,index=['Co-efficient']).transpose()
w = pd.DataFrame(x.columns, columns=['attribute'])
Step 8: Concatenating the DataFrames to compare
coeff_d2020 = pd.concat([w,v], axis=1, join='inner')
coeff_d2020
| attribute | Co-efficient | |
|---|---|---|
| 0 | GDP per capita | 1.166126e-01 |
| 1 | Social support | 2.181179e+00 |
| 2 | Healthy life expectancy | 1.063904e+05 |
| 3 | Freedom | 2.092947e+00 |
| 4 | Generosity | 3.345929e-01 |
| 5 | Perceptions of corruption | -9.598309e-01 |
| 6 | Health | -2.955160e+06 |
Step 9:Comparing the predicted value to the actual value
import numpy as np
y_pred = regressor.predict(x_test)
y_pred = pd.DataFrame(y_pred, columns=['Predictions'])
y_pred.head(3)
| Predictions | |
|---|---|
| 0 | 5.395633 |
| 1 | 5.862217 |
| 2 | 5.259823 |
from sklearn import metrics
import numpy as np
print('Mean Absolute Error:', metrics.mean_absolute_error(y_test, y_pred))
print('Mean Squared Error:', metrics.mean_squared_error(y_test, y_pred))
print('Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
Mean Absolute Error: 0.3962943704844692
Mean Squared Error: 0.2837987519155517
Root Mean Squared Error: 0.5327276526664931
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.sandbox.regression.predstd import wls_prediction_std
np.random.seed(9876789)
Fit and summary:
model = sm.OLS(y, x)
results = model.fit()
print(results.summary())
OLS Regression Results
=======================================================================================
Dep. Variable: Ladder score R-squared (uncentered): 0.990
Model: OLS Adj. R-squared (uncentered): 0.990
Method: Least Squares F-statistic: 2082.
Date: Sat, 14 Nov 2020 Prob (F-statistic): 7.81e-143
Time: 22:51:37 Log-Likelihood: -127.33
No. Observations: 153 AIC: 268.7
Df Residuals: 146 BIC: 289.9
Df Model: 7
Covariance Type: nonrobust
=============================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------------------
GDP per capita 0.2291 0.082 2.791 0.006 0.067 0.391
Social support 2.7233 0.661 4.119 0.000 1.417 4.030
Healthy life expectancy -0.0103 0.015 -0.689 0.492 -0.040 0.019
Freedom 1.7768 0.498 3.571 0.000 0.794 2.760
Generosity 0.4106 0.337 1.218 0.225 -0.256 1.077
Perceptions of corruption -0.6282 0.315 -1.995 0.048 -1.250 -0.006
Health 1.2655 0.393 3.219 0.002 0.488 2.043
==============================================================================
Omnibus: 7.971 Durbin-Watson: 1.482
Prob(Omnibus): 0.019 Jarque-Bera (JB): 7.701
Skew: -0.503 Prob(JB): 0.0213
Kurtosis: 3.441 Cond. No. 1.02e+03
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.02e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
Testing the model
tmodel = sm.OLS(y_test, x_test)
resultt = tmodel.fit()
print(resultt.summary())
OLS Regression Results
=======================================================================================
Dep. Variable: Ladder score R-squared (uncentered): 0.994
Model: OLS Adj. R-squared (uncentered): 0.993
Method: Least Squares F-statistic: 938.9
Date: Sat, 14 Nov 2020 Prob (F-statistic): 2.09e-41
Time: 22:51:41 Log-Likelihood: -26.099
No. Observations: 46 AIC: 66.20
Df Residuals: 39 BIC: 79.00
Df Model: 7
Covariance Type: nonrobust
=============================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------------------
GDP per capita 0.3581 0.114 3.150 0.003 0.128 0.588
Social support 3.6510 0.952 3.834 0.000 1.725 5.577
Healthy life expectancy -0.0550 0.022 -2.555 0.015 -0.099 -0.011
Freedom 1.9445 0.778 2.499 0.017 0.370 3.519
Generosity 0.2116 0.614 0.345 0.732 -1.030 1.453
Perceptions of corruption -0.2617 0.480 -0.546 0.588 -1.232 0.709
Health 2.0042 0.687 2.915 0.006 0.614 3.395
==============================================================================
Omnibus: 3.039 Durbin-Watson: 1.771
Prob(Omnibus): 0.219 Jarque-Bera (JB): 2.374
Skew: 0.117 Prob(JB): 0.305
Kurtosis: 4.088 Cond. No. 1.02e+03
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.02e+03. This might indicate that there are
strong multicollinearity or other numerical problems.